Question

Write the equation of the circle graphed below

Answer 1

`(x-1)^2+(y+1)^2=0.25`

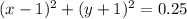
Explanation:

From the given graph it is clear that the center of the circle is (1,-1) and the circle passing through the point (0.5,-1).

So, radius of the circle is

`r=√((x_2-x_1)^2+(y_2-y_1)^2)`

`r=√((0.5-1)^2+(-1-(-1))^2)`

`r=√((-0.5)^2)`

`r=√((0.5)^2)`

`r=0.5`

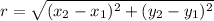
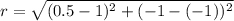
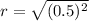
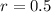
The radius of the circle is 0.5 units.

The standard form of a circle is

`(x-h)^2+(y-k)^2=r^2`

where, (h,k) is center and r is radius.

The center of given circle is (1,-1) and radius is 0.5. So, the equation of circle is

`(x-(1))^2+(y-(-1))^2=(0.5)^2`

`(x-1)^2+(y+1)^2=0.25`

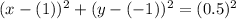
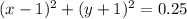
Therefore, the required equation is
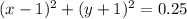`(x-1)^2+(y+1)^2=0.25`.