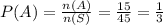Question

A point $(x, y)$ with integer coordinates is randomly selected such that $0 \le x \le 8$ and $0 \le y \le 4$. what is the probability that $x + y \le 4$? express your answer as a common fraction.

Answer 1

`(1)/(3)`

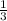
Explanation:

A point (x, y) with integer coordinates is randomly selected such that
`0 \le x \le 8 \:and\: $0 \le y \le 4$.`

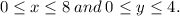
The possible pairs of (x,y) are:

(0,0),(0,1),(0,2),(0,3),(0,4)

(1,0),(1,1),(1,2),(1,3),(1,4)

(2,0),(2,1),(2,2),(2,3),(2,4)

(3,0),(3,1),(3,2),(3,3),(3,4)

(4,0),(4,1),(4,2),(4,3),(4,4)

(5,0),(5,1),(5,2),(5,3),(5,4)

(6,0),(6,1),(6,2),(6,3),(6,4)

(7,0),(7,1),(7,2),(7,3),(7,4)

(8,0),(8,1),(8,2),(8,3),(8,4)

The Total Possible Outcomes n(S)= 45

The pair (x, y) that satisfies the given condition (say event A:
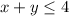`x + y \le 4`) are:

`(0,0),(0,1),(0,2),(0,3),(0,4)\\(1,0),(1,1),(1,2),(1,3)\\(2,0),(2,1),(2,2)\\(3,0),(3,1)\\(4,0)`

n(A)=15

Therefore:

`P(A)=(n(A))/(n(S)) =(15)/(45) =(1)/(3)`