Question

Write the equation x2−4x=−12 in standard form. =0 Question 2 Identify the values of a,b, and c that you would use to solve the equation using the Quadratic Formula. a= b= c=

Answer 1

a = 1

b = -4

c = 12

Solutions to the equation are;

x = 2-2·i·√2 or x = 2+2·i·√2

Explanation:

The given equation is x² - 4x = -12

In standard form we have;

x² - 4·x + 12 = 0

In the above equation, we have our a = 1

b = -4

c = 12

To solve the quadratic equation with the quadratic formula, we have;

x =
`(-b \pm √(b^2 -4ac) )/(2a)`

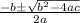
Plugging in the values we have;

`(-(-4) \pm √((-4)^2 -4* 1 * 12) )/(2* 1)= (4 \pm √((-32) )/(2) = 2 \pm 2√(-2)`

The solutions are x = 2-2·i·√2 or x = 2+2·i·√2.

Answer 2

The values for a, b c are:

a = 1

b = -4

c = 12

Explanation:

In order to make it in standard form we need to swap the "-12" to the left side. When we swap numbers from one side to the other of an equation we need to invert their operation so the equation will still be valid, so in this case the number "-12" will go to the left side as "+12". We have:

x² - 4x + 12 = 0

The values for a, b c are:

a = 1

b = -4

c = 12