Question

A rocket is shot straight up from a 30-foot

rooftop with an initial velocity of 128 feet

per second. The height, h, of the rocket is

given by the equation h = -16t^2+ 128t+ 30,

where t is the time elapsed in seconds and h

is the height in feet.

a. How long will it take the rocket to

return to the ground?

b. The maximum height that the rocket

achieves is 286 feet. At what time does

it reach that height?

Answer 1

a) The rocket will taket 8.2278 seconds to return to the ground.

b) The rocket reaches 286 feet at 4 seconds.

Explanation:

Consider the following, if we have a two degree polynomial of the form
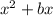`x^2+bx` we can complete the square by adding and substracting the following term

`x^2+bx=  x^2+bx + ((b)/(2))^2- ((b)/(2))^2= (x-(b)/(2))^2-((b)/(2))^2`.

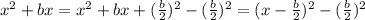Then, consider the following algebraic manipulation

`h(t) = -16t^2+128t+30 = -16(t^2-8t)+30`

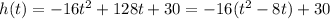
If we complete the square, then

`h(t) = -16(t^2-8t+((8)/(2))^2-((8)/(2))^2)+30 = -16(t^2-8t +16)+30+16^2 = -16(t-4)^2+286`

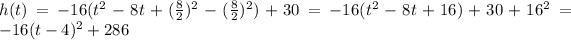
b) From this expression, we must find the value of t for which h(t) = 286. It can easily be found that at t=4 we have that h(t) = 286.

a). We want to find to for which h(t)=0 (the rocket is at the ground). Then

`h(t) = -16(t-4)^2+286=0`

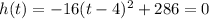
Thus

`(t-4)^2 = (-286)/(-16) = (286)/(16)`

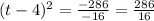
Then,
`t = \pm\sqrt[]{(286)/(16)}+4`. Since t must be positive, we must have that

`t = \sqrt[]{(286)/(16)}+4= 8.2278`