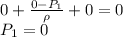Question

Air flows through a rectangular section Venturi channel . The width of the channel is 0.06 m; Theheight at the inlet (1) and outlet (4) is 0.04 m. The height (3) in

the Bosphorus is 0.02 m. Compressibility and viscous effects can
be ignored (ρwater = 1000 kg / m3, ρ air = 1.23 kg / m3)
a) Calculate the flow rate if the
water in the small tube connected to the static pressure tap in the throat is drawn as 0.10 m as shown?
b)Calculate the height (h2) in section (2) according to the flow rate you find in part a .
c)Calculate the pressure at the inlet (1) for the fluid to flow ( according to the values you find in a and b )?

Answer 1

a) The flow rate if the water is 0.0553 m³/s

b) The height is 0.0253 m

c) The pressure at the inlet 1 is 0

Step-by-step explanation:

Given:

Width of the channel is 0.06 m

Height at 1 and 4 is 0.04 m

Height at 3 is 0.02 m

ρwater = 1000 kg/m³

ρair = 1.23 kg/m³

Questions:

a) The flow rate if the water in the small tube connected to the static pressure tap, Q = ?

b) Calculate the height in section 2, h₂ = ?

c) Calculate the pressure at the inlet (1) for the fluid to flow, P₁ = ?

a) To solve this question, you need to apply the Bernoulli's equation between the points 3 and 4:

`(P_(4)-P_(3) )/(\rho _(air) ) +(v_(4)^(2) -v_(3)^(2) )/(2 ) +g(z_(4) -z_(3) )=0`

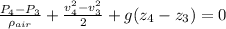
Here,

P₄ = 0 (open at atmosphere)

z₄-z₃ = 0 (same height)

P₃ = ρgh₃ = 1000*9.8*0.1 = 980

Substituting values and solving for v₄

`v_(4) =\sqrt{(2P_(3) )/(3\rho _(air) ) } =\sqrt{(2*980)/(3*1.23) } =23.047m/s`

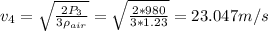
The flow rate

`Q=A_(4) v_(4) =0.06*0.04*23.047=0.0553m^(3) /s`

b) Applying the Bernoulli's equation between the points 2 and 4

`g(z_(4) -z_(2) )+(P_(4)-P_(2) )/(\rho ) +(v_(4)^(2)-v_(2)^(2) )/(2) =0`

z₄ - z₂ = 0 (same height)

P₄ = 0 (open at atmosphere)

`0+(1000*9.8*0.05)/(1.23) +(23.047^(2)-v_(2)^(2) )/(2) =0`

Solving for v₂

v₂ = 36.5 m/s

To get the height you need to use the continuity expression

`v_(4) A_(4) =v_(2) A_(2)`

`23.047*0.06*0.04=36.5*0.06*h_(2)`

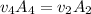
Solving for h₂

h₂ = 0.0253 m

c) In this part, you need to apply the Bernoulli's expression between the points 1 and 4

`g(z_(4) -z_(1) )+(P_(4)-P_(1) )/(\rho ) +(v_(4)^(2)-v_(1)^(2) )/(2) =0`

Here

z₄-z₁ = 0, same height

v₄-v₁ = 0, same speeds

P₄ = 0, open atmosphere

Substituting values:

`0+(0-P_(1) )/(\rho ) +0=0\\P_(1) =0`