Question

This coming summer, I’m planning an epic road trip to the National Parks of the American West (Yosemite, Lassen Volcanic, Glacier, etc.). Driving in such rugged, dangerous terrain is hard on one’s car, so I plan to install a new fan belt in my car right before I leave, and to carry two extra (new) fan belts on the trip. Given the conditions, the manufacturer of the belt expects it will break on a given day with a 2% probability. Assume belt breaks are independent from day to day and that any time the belt breaks, I spend that day replacing it with one of the spare belts, and then begin driving again the next day. My trip ends when all the belts break.The worst case scenario for my trip is that a belt breaks on each of the first three days, although this is very unlikely. What does the belt-break probability need to be for there to be a 50% chance of this worst-case scenario?

Answer 1

Check the explanation

Explanation:

Let p denote the probability that a fan belt breaks during the trip so, the probability that fan belt breaks consecutively on theses days is the probability
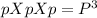`pXpXp=P^3`the worst case scenario is that belt breaks on 3 consecutive days.this is having 50% or 0.5 probability of happening

⇒
`P^3 = 0.5`

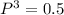
P=
`\sqrt[3]{0.50}` =
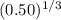`(0.50)^(1/3)` =0.7937

Hence p needs to be 79.37% or probability that fan belt breaks on a day is 79.37%

Here
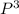`P^3` is probability that fan belt breaks on 3 consecutive days because probability of the events can be multiplied.