Question

Kaylee invested $910 in an account paying an interest rate of 2.6% compounded

quarterly. Assuming no deposits or withdrawals are made, how much money, to the
nearest dollar, would be in the account after 10 years?

Answer 1

A≈1179

Explanation:

Answer 2

$1,179

Explanation:

Lets use the compound interest formula provided to solve this:

`A=P(1+(r)/(n) )^(nt)`

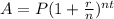
P = initial balance

r = interest rate (decimal)

n = number of times compounded annually

t = time

First, lets change 2.6% into a decimal:

2.6% ->
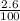`(2.6)/(100)` -> 0.026

Since the interest is compounded quarterly, we will use 4 for n. Lets plug in the values now:

`A=910(1+(0.026)/(4))^(4(10))`

`A=1,179.21`

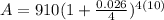
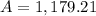
The account balance after 10 years will be $1,179