Question

A small publisher wishes to publish self-improvement books. After a survey of the market, the publisher finds that the average cost of the type of book that she wishes to publish is $15.00. If she wants to price her books to sell in the middle 64% range, what should the maximum and minimum prices of the books be? The standard deviation is $0.25 and the variable is normally distributed.

Answer 1

Maximum price of book will be $15.23

Minimum price of book will be $14.77.

Explanation:

We are given that a small publisher wishes to publish self-improvement books. After a survey of the market, the publisher finds that the average cost of the type of book that she wishes to publish is $15.00. The standard deviation is $0.25 and the variable is normally distributed.

Also, she wants to price her books to sell in the middle 64% range.

The above situation represents that we want 64% confidence interval for the price of book which she wants to publish.

Firstly, the pivotal quantity for 64% confidence interval for the population mean is given by;

P.Q. =
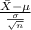`(\bar X -\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample average cost of the type of book = $15

`\sigma` = population standard deviation = $0.25

n = sample of book = 1

`\mu` = population mean

Here level of significance =
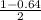`(1-0.64)/(2)` = 18%

Here for constructing 64% confidence interval we have used One-sample z test statistics because we know about population standard deviation.

So, 64% confidence interval for the population mean,
`\mu` is ;

P(-0.9195 < N(0,1) < 0.9195) = 0.64 {As the critical value of z at 18%

level of significance are -0.9195 & 0.9195}

P(-0.9195 <
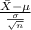`(\bar X -\mu)/((\sigma)/(√(n) ) )` < 0.9195) = 0.64

P(
`-0.9195 * {(\sigma)/(√(n) ) }` <
`{\bar X -\mu}` <
`0.9195 * {(\sigma)/(√(n) ) }` ) = 0.64

P(
`\bar X-0.9195 * {(\sigma)/(√(n) ) }` <
`\mu` <
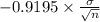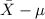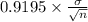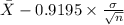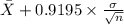`\bar X+0.9195 * {(\sigma)/(√(n) ) }` ) = 0.64

64% confidence interval for
`\mu` = [
`\bar X-0.9195 * {(\sigma)/(√(n) ) }` ,
`\bar X +0.9195 * {(\sigma)/(√(n) ) }` ]

= [
`15-0.9195 * {(0.25)/(√(1) ) }` ,
`15-0.9195 * {(0.25)/(√(1) ) }` ]

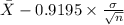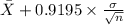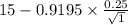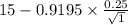= [$14.77 , $15.23]

Therefore, the maximum price of book will be $15.23 and the minimum price of book will be $14.77.