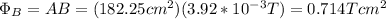Question

A single-turn square loop of side L is centered on the axis of a long solenoid. In addition, the plane of the square loop is perpendicular to the axis of the solenoid. The solenoid has 1250turns per meter and a diameter of 6.00 cm, and carries a current of 2.50 A. Find the magnetic flux through the loop when (a) LPart A: Find the magnetic flux through the loop when L= 2.75 cm .

Part B: Find the magnetic flux through the loop when L= 5.60 cm .


Part C: Find the magnetic flux through the loop when L= 13.5 cm .

Answer 1

a) 0.029Tcm^2

b) 0.122Tcm^2

c) 0.714Tcm^2

Step-by-step explanation:

To find the magnetic flux in the loop it is necessary to calculate the magnetic field generated by the solenoid. This is calculated by using the following formula:

`B=\mu_o N I`

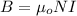
mu_o: magnetic permeability of vacuum = 4pi*10^{-7}T/A

N: turns of the solenoid = 1250

I: current in the solenoid = 2.50A

By replacing all these values you obtain

`B=(4\pi*10^(-7)T/A)(1250)(2.50A)=3.92*10^(-3)T=3.92mT`

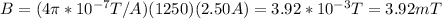
To know what is the flux in the loop, you take into account that the effective area of the loop, in which the magnetic field crosses it, is determined by the cross area of the solenoid. Hence, you compute the cross area of the solenoid:

`A_s=\pi(6.00cm)^2=113.09cm^2`

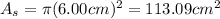
This is the maximum value for the effective area of the loop:

a) for L=2.75cm -> A = 7.56cm^2. The area of the loop is lower than the As. Hence, you use the area of the loop:

`\Phi_B=AB=(7.56cm^2)(3.92*10^(-3)T)=0.029Tcm^2`

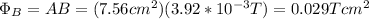
b) for L=5.60cm -> A = 31.36cm^2. The same as before:
`\Phi_B=AB=(31.36cm^2)(3.92*10^(-3)T)=0.122Tcm^2`

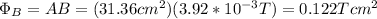
c) for L=13.5cm -> A = 182.25cm^2. This value is higher than As. Hence you use As:

`\Phi_B=AB=(182.25cm^2)(3.92*10^(-3)T)=0.714Tcm^2`