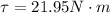Question

A square metal plate 2.5m on each side is pivoted about an axis though point O at its center and perpendicular to the plate. Calculate the net torque due to the three forces if the magnitudes of the forces are F1=18N, F2=20N, and F3=11N..

Answer 1

Complete Question

The diagram for this question is shown on the first uploaded image

Answer:

The net torque
`\tau = 21.95N \cdot m`

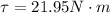
Step-by-step explanation:

From the question we are told that

The length of each side is
`L = 2.5 m`

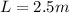
The first force is
`F_1 = 18N`

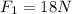
The second force is
`F_2 = 20 N`

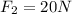
The third force is
`F_3 = 11N`

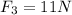
The free body diagram for the question is shown on the second uploaded image

Generally torque is mathematically represented as

`\tau = r * F`

Where
`\tau` is the torque

r is the length from the rotating point to the point the force is applied, this is also the radius of the circular path made

F is the force causing the rotation.

looking at the free body diagram we can deduce that L is the diameter of the circular path made as a result of toque

Now for the torque due to force
`F_1`

`\tau_1 = - F_1 * r_1`

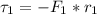
The negative sign is because the direction of
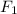`F_1` is clockwise

=>
`\tau_1 = - F_1 * (L)/(2)`

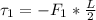
Substituting value

`\tau_1 = - 18 * (2.5)/(2 )`

`\tau_1 = - 22.5 N \cdot m`

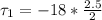
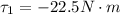
The torque as a result of the second force is mathematically evaluated as

`\tau_2 = F_2 * r_2`

`\tau_2 = F_2 * (L)/(2)`

`= 20 * (2.5)/(2)`

`\tau_ 2 = 25 \ N \cdot m`

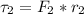
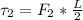
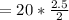
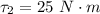
The torque as a result of the third force is mathematically evaluated as

`\tau_3 =r_3 (F_3 sin \theta + F_3 cos \theta )`

`\tau_3 = (L)/(2) (F_3 sin \theta + F_3 cos \theta )`

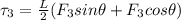
Where the free body diagram
`\theta = 45^o`

`\tau_3 = (2.5)/(2) (11 * sin (45) +11 cos (45) )`

`\tau_ 3 = 19.45 \ N \cdot m`

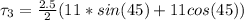
The net torque the mathematically

`\tau = \tau_1 + \tau_2 + \tau_3`

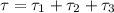
substituting value

`\tau = -22.5 + 25 + 19.45`

`\tau = 21.95N \cdot m`