Answer:
There are two possible values for r (area): r =-7 or r=3
Explanation:
Given the rectangular rug area is:
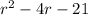
We have to convert the above equation into factored form.
So two numbers whose product is -21r² and sum is -4r
<=>
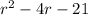
=
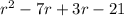
= r (r -7) + 3(r -7)
= (r-7)(r+3)
We set
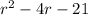 = 0
= 0
<=> (r-7)(r+3) = 0
<=> (r-7) = 0 or (r+3) = 0
<=> r =-7 or r=3
So, there are two possible values for r (area): r =-7 or r=3