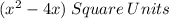Question

A square has sides with lengths of (x - 2) units. A rectangle has a length of x units and a width of

(x - 4) units.

Which statements about the situation are true? Select all that apply.

The area of the square is greater than the area of the rectangle.

B

The area of the square is (x2 - 4) square units.

The value of x must be greater than 4.

The difference in the areas is 4x -4.

The area of the rectangle is (x2 - 4x) square units.

Answer 1

(A)The area of the square is greater than the area of the rectangle.

(C)The value of x must be greater than 4

(E)The area of the rectangle is
`(x^2-4x) \:Square \:Units`

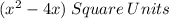
Explanation:

The Square has side lengths of (x - 2) units.

Area of the Square

`(x-2)^2=(x-2)(x-2)=x^2-2x-2x+4\\=(x^2-4x+4) \:Square \:Units`

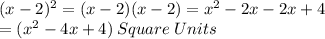
The rectangle has a length of x units and a width of (x - 4) units.

Area of the Rectangle =
`x(x-4)=(x^2-4x) \:Square \:Units`

The following statements are true:

(A)The area of the square is greater than the area of the rectangle.

This is because the area of the square is an addition of 4 to the area of the rectangle.

(C)The value of x must be greater than 4

If x is less than or equal to 4, the area of the rectangle will be negative or zero.

(E)The area of the rectangle is
`(x^2-4x) \:Square \:Units`