Question

Two similar cones have volume of 343pi cubic centimeters and 512pi cubic centimeters. The height of each cone is equal to 3 times its radius. Find the radius and height of both cones

Answer 1

For the first cone: r = 7 cm, h = 21 cm

For the second cone: r = 8 cm, h = 24 cm

Explanation:

The volume of the first cone is
`343\pi cm^3`

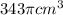
The volume of the second cone is
`512\pi cm^3`

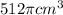
We are told that the height of each cone is 3 times its radius, hence:

h = 3r

The volume of a cone is given as:

`V = (1)/(3) \pi r^2h`

Substituting h = 3r:

`V = (1)/(3) \pi r^2(3r)\\\\\\V = (1)/(3) \pi (3r^3)\\\\\\V = \pi r^3`

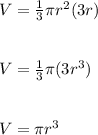
For the first cone, V =
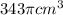`343\pi cm^3`, radius, r, will be:

`343\pi = \pi r^3\\\\\\=> r^3 = 343\\\\\\r = \sqrt[3]{343} \\\\\\r = 7 cm`

∴ Its height will be:

h = 3r = 3 * 7 = 21 cm

For the second cone, V =
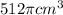`512\pi cm^3`, radius, r, will be:

`512\pi = \pi r^3\\\\\\=> r^3 = 512\\\\\\r = \sqrt[3]{512} \\\\\\r = 8 cm`

∴ Its height will be:

h = 3r = 3 * 8 = 24 cm

The radius and height of the first cone are 7 cm and 21 cm respectively while the radius and height of the second cone are 8 cm and 24 cm respectively.