Question

A study by Consumer Reports showed that 64% of supermarket shoppers believe supermarket brands to be as good as national name brands. To investigate whether this result applies to its own product, the manufacturer of a national name-brand ketchup asked a sample of shoppers whether they believed that supermarket ketchup was as good as the national brand ketchup.

a. Formulate the hypotheses that could be used to determine whether the percentage of supermarket shoppers who believe that the supermarket ketchup was as good as the national brand ketchup differed from 64%.

b. If a sample of 100 shoppers showed 52 stating that the supermarket brand was as good as the national brand, what is the p-value (to 4 decimals)?

c. At = α= 0.05, what is your conclusion?

d. Should the national brand ketchup manufacturer be pleased with this conclusion?

Answer 1

a) As the claim is that the percentage of supermarket shoppers who believe that the supermarket ketchup was as good as the national brand ketchup differs from 64% , the percentage can be significantly highly or lower. Then, the test is two-tailed and the null and alternative hypothesis are:

`H_0: \pi=0.64\\\\H_a:\pi\\eq 0.64`

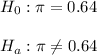
b) P-value = 0.0166

c) At α= 0.05, the null hypothesis is rejected.

There is enough evidence to support the claim that the percentage of supermarket shoppers who believe that the supermarket ketchup was as good as the national brand ketchup differs from 64% .

d) No, as its brand is below the average when it comes to approval of the consumers.

Explanation:

This is a hypothesis test for a proportion.

The claim is that the percentage of supermarket shoppers who believe that the supermarket ketchup was as good as the national brand ketchup differs from 64% .

Then, the null and alternative hypothesis are:

`H_0: \pi=0.64\\\\H_a:\pi\\eq 0.64`

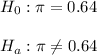
The significance level is 0.05.

The sample has a size n=100.

The sample proportion is p=0.52.

`p=X/n=52/100=0.52`

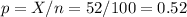
The standard error of the proportion is:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.64*0.36)/(100)}\\\\\\ \sigma_p=√(0.0023)=0.048`

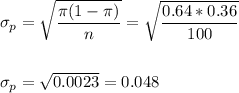
Then, we can calculate the z-statistic as:

`z=(p-\pi-0.5/n)/(\sigma_p)=(0.52-0.64+0.5/100)/(0.048)=(-0.115)/(0.048)=-2.3958`

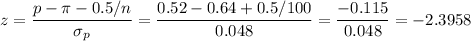
This test is a two-tailed test, so the P-value for this test is calculated as:

`P-value=2\cdot P(z<-2.3958)=0.0166`

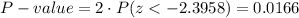
As the P-value (0.0166) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that the percentage of supermarket shoppers who believe that the supermarket ketchup was as good as the national brand ketchup differs from 64% .