Question

A town has a population of 17000 and grows at 3% every year. To the nearest year, how long will it be until the population will reach 20400

Answer 1

6

Explanation:

deltamath

Answer 2

The population will reach 20,400 after 6 years.

Explanation:

Exponential function:

`y(t)=y_0(1+r)^t`

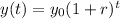
y(t)= Population after t years

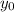`y_0` = initial population

r= rate of grow

t= time.

A town has a population of 17,000 and grows at a rate 3% every year.

y(t)= 20,400,
`y_0` = 17,000, r=3%=0.03, t=?

`20,400=17,000(1+0.03)^t`

`\Rightarrow (20,400)/(17,000)=(1.03)^t`

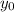`\Rightarrow (102)/(85)=(1.03)^t`

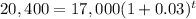
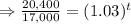
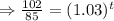
Taking ln function both sides

`\Rightarrow ln|(102)/(85)|=ln|(1.03)^t|`

`\Rightarrow ln|(102)/(85)|=t\ ln|(1.03)|`

`\Rightarrow t=(ln|(102)/(85)|)/(\ ln|(1.03)|)`

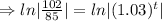
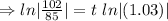
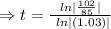
⇒ t = 6 year.

The population will reach 20,400 after 6 years.