Answer:
Explanation:
let the quadratic eq. be ax²+bx+c=0
or x²+b/a x+c/a=0
or x²+b/ax=-c/a
to complete the square add both sides (b/2a)²or b²/4a²
x²+b/a x+(b/2a)²=b²/4a² -c/a
(x+b/2a)²=(b²-4ac)/(4a²)
taking square root
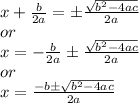
now you must know why -b and not +b