Explanation:
A,B, and C are collinear, and B is between A and C. The ratio of AB to BC is 1:1 of A IS AT (-1,9) and B (2,0)
to find out point C use section formula
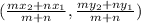
A is (-1,9) that is our (x1,y1)
that is our (x2,y2)
ratio is 1:1 that is m and n
Plug in the values in the formula
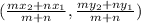
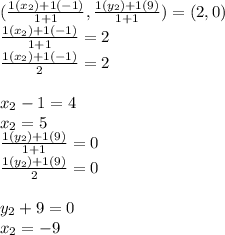
Answer C is (5,-9)