Answer:
a) P(X≥143)=0
b) This contradicts the study as getting a sample with this proportion is almost impossible (if the proportion of 68% is true).
Explanation:
If we use the normal approximation to the binomial distribution we have the following parameters (mean and standard deviation):
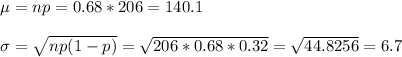
Then, we can calculate the probability of X being equal or more than 143 using the z-score:
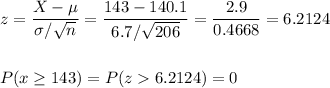
This contradicts the study as getting a sample with this proportion is almost impossible (if the proportion of 68% is true).