Question

The height of a triangle is 2 less than 5 times its base. If the base of the triangle is xfeet, and the area is 12 square feet, which equation mofles this situation

Answer 1

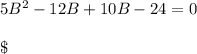`5B^(2) - 12B +10B - 24 = 0\\\\\` Base of triangle = 2.4 Feet and Height of triangle = 10 feet.

Explanation:

This problem can be solved by using formula to calculate area of triangle.

Area of triangle = 1/2*(base*height)

given

Let base of triangle B

height if triangle H

according to problem

The height of a triangle is 2 less than 5 times its base

mathematically it can be expressed as

H = 5*B - 2

Given area of triangle= 12 sq feet

Area of triangle = 1/2*(base*height)

=> 12 = 1/2* {B*(5*B-2)}

=> 24 = 5B^2 - 2B

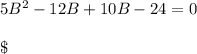`5B^(2) - 12B +10B - 24 = 0\\\\\` which is a quadratic equation

It can be solved as given below

`5B^(2) +10B - 12B - 24 = 0\\\\\=>5B(B +2) -12(B +2) = 0\\=> (5B - 12) (B +2) = 0\\5B - 12 = 0 or B + 2 = 0\\Hence B = 12/5 \ or \ B = -2\\\\`

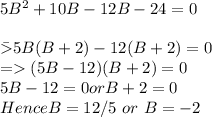
Since for side of triangle B cannot be negative number hence B= 12/5 = 2.4

Therefore height of triangle = 5*B - 2 = 5*2.4 - 2 = 12 - 2 = 10

Base of triangle = 2.4 Feet and Height of triangle = 10 feet.

Equation which models this situation is

`5B^(2) - 12B +10B - 24 = 0\\\\\`