Question

If testing the claim that sigma subscript 1 superscript 2 baseline not equals sigma subscript 2 superscript 2σ21≠σ22​, what do we know about the two samples if the test statistic is fequals=​1?

Answer 1

The statistic for this system of hypothesis is given by:

`F=(s^2_1)/(s^2_2)`

If the statistic is equal to 1 then that means
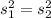`s^2_1 = s^2_2` and we don't have enough evidence to conclude that the two population variances and deviations are different.

Explanation:

System of hypothesis

We want to test if the variation for a group1 is equal to another one 2, so the system of hypothesis are:

H0:
`\sigma^2_1 = \sigma^2_2`

H1:
`\sigma^2_1 \\eq \sigma^2_2`

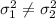
Calculate the statistic

The statistic for this system of hypothesis is given by:

`F=(s^2_1)/(s^2_2)`

If the statistic is equal to 1 then that means
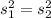`s^2_1 = s^2_2` and we don't have enough evidence to conclude that the two population variances and deviations are different.