Question

Find the surface area of the solid formed by the net. Round your answer to the nearest hundredth.

Answer 1

The area of the total figure is around 535.43 square centimeters.

Explanation:

In the image attached, you can notice that all rectangles have a base of 20 centimeters.

Also, each side of the equilaterals triangles is 8 centimeters.

Notice that the height of each rectangle is equal to a side of a triangle.

Using all given vales, the area of each rectangle is

`A_(rectangle)=b* h=20 * 8 =160 cm^(2)`

The area of all rectangles is

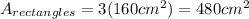`A_(rectangles)=3(160cm^(2))=480 cm^(2)`, because there are three rectangles in total.

The area of each triangle is

`A_(triangle )=(√(3) )/(4) (8cm)^(2) =(√(3) )/(4)(64cm^(2) )\\A_(triangle )=16√(3) cm^(2)`

The area of both triangles is

`A_(triangles)=2(16√(3)cm^(2) )=32√(3) cm ^(2)`

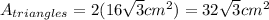
Now, the area of the whole figure is the sum of the area of triangles and rectangles

`A_(total)=480cm^(2) +32√(3) cm^(2) \approx 535.43 cm^(2)`

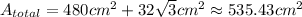
Therefore, the area of the total figure is around 535.43 square centimeters.