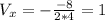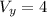Question

The function f(t) = 4t2 − 8t + 8 shows the height from the ground f(t), in meters, of a roller coaster car at different times t. Write f(t) in the vertex form a(x − h)2 + k, where a, h, and k are integers, and interpret the vertex of f(t). (1 point)

Answer 1

`f(t) = 4(t-1)^2 +4`

So then we see that the required values are:

`a = 4, h =1, k =4`

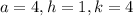
And the vertex for this case would be:

`V_x = -(-8)/(2*4) = 1`

`V_y = 4`

`V(1,4)`

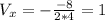
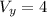
Explanation:

For this case we have the following function given:

`f(t) = 4t^2 -8t +8`

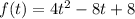
And we want to wrote this equation in the form a(x − h)2 + k

We can divide both sides of the equation and we got:

`(f(t))/(4) = t^2 -2t +2`

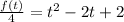
Now we can comple the square in the rigth part with this:

`(f(t))/(4) = t^2 -2t +1 +(2-1)`

`(f(t))/(4) = (t^2 -2t +1) +(2-1)= (t-1)^2 +1`

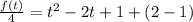
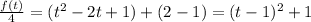
And now we can multiply both sides by 4 and we got:

`f(t) = 4(t-1)^2 +4`

So then we see that the required values are:

`a = 4, h =1, k =4`

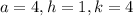
And the vertex for this case would be:

`V_x = -(-8)/(2*4) = 1`

`V_y = 4`

`V(1,4)`