Question

Element X decays radioactively with a half life of 11 minutes. If there are 870 grams of Element X, how long, to the nearest tenth of a minute, would it take the element to decay to 154 grams?

Answer 1

60.6 minutes

Explanation:

--------------------------------

Answer 2

It would take 27.5 minutes the element to decay to 154 grams.

Explanation:

The decay equation:

`\frac {dN}{dt}\propto -N`

`\Rightarrow \R\frac {dN}{dt}=-\lambda N`

`\Rightarrow \frac {dN}N=-\lambda dt`

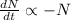
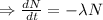
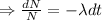
Integrating both sides

`\Rightarrow \int \frac {dN}N=\int-\lambda dt`

`\Rightarrow ln|N|=-\lambda t+c`

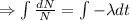
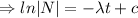
When t=0, N=
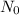`N_0` = initial amount

`ln|N_0|=-\lambda .0+c`

`\Rightarrow c=ln|N_0|`

`ln|N|=-\lambda t+ln|N_0|`

`\Rightarrow ln|N|-ln|N_0|=-\lambda t`

`\Rightarrow ln|(N)/(N_0)|=-\lambda t`

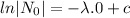
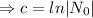
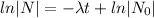
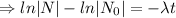
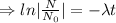
Decay equation:

`ln|(N)/(N_0)|=-\lambda t`

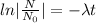
Given that, the half life of of element X is 11 minutes.

For half life,
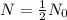`N=\frac12 N_0`, t= 11 min.

`ln|(N)/(N_0)|=-\lambda t`

`\Rightarrow ln|(\frac12N_0)/(N_0)|=-\lambda . 11`

`\Rightarrow ln|\frac12}|=-\lambda . 11`

`\Rightarrow -\lambda . 11=ln|\frac12}|`

`\Rightarrow \lambda =(ln|\frac12|)/(-11)`

`\Rightarrow \lambda =(ln|2|)/(11)` [
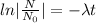
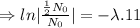
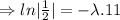
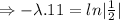
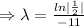
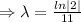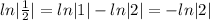`ln|\frac12|=ln|1|-ln|2|=-ln|2|` , since ln|1|=0]

N=154 grams,
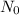`N_0` = 870 grams, t=?

`ln|(N)/(N_0)|=-\lambda t`

`\Rightarrow ln|(154)/(870)|=-(ln|2|)/(11).t`

`\Rightarrow t= (ln|(154)/(870)|* 11)/(-ln|2|)`

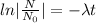
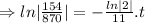
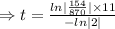
=27.5 minutes

It would take 27.5 minutes the element to decay to 154 grams.