We have been given that the ages of students in a school are normally distributed with a mean of 15 years and a standard deviation of 2 years.
We are asked to find the percentage of students that are between 14 and 18 years old.
First of all, we will find z-score corresponding to 14 and 18 using z-score formula.

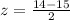
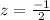

Similarly, we will find the z-score corresponding to 18.

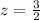
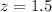
Now we will find the probability of getting a z-score between
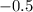 and
and
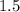 that is
that is
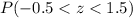 .
.
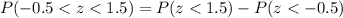
Using normal distribution table, we will get:
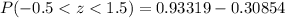
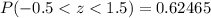
Let us convert
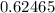 into percentage.
into percentage.
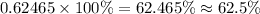
Therefore, approximately
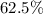 of the students are between 14 and 18 years old.
of the students are between 14 and 18 years old.