Question

Hello people ~

The given figure shows a cone of height "h cm" and base-radius "r cm" that is made from a wooden spherical solid of radius 10 cm. The volume of the cone is cm³.

(a) Show that r² =20h-h²

(b) Express V in terms of h

(c) Hence, find the value of h such that the volume of the cone is a maximum.​

Answer 1

(a) see step-by-step

`\textsf{(b)}\quad V=(20)/(3) \pi h^2-\frac13 \pi h^3`

`\textsf{(c)}\quad h=(40)/(3)`

Explanation:

Part (a)

A right triangle can be drawn with vertices at the center O, the base angle of the cone and the center of the base of the cone (see annotated image).

Side lengths of the formed right triangle:

• Hypotenuse = radius of sphere = 10 cm
• Height = height of cone - radius of sphere = (h - 10) cm
• Base = base radius of cone = r cm

Using Pythagoras' Theorem
`a^2+b^2=c^2`
(where a and b are the legs, and c is the hypotenuse, of a right triangle)

`\implies r^2+(h-10)^2=10^2`

`\implies r^2+h^2-20h+100=100`

`\implies r^2+h^2-20h=0`

`\implies r^2=20h-h^2`

Part (b)

`\textsf{Volume of a cone}=\frac13 \pi r^2h`
(where r is the radius and h is the height)

Substitute the expression for
`r^2` found in part (a) into the equation so that volume (V) is expressed in terms of h:

`\begin{aligned}V & =\frac13 \pi r^2h\\\\ \implies V & =\frac13 \pi (20h-h^2)h\\\\ & = \frac13 \pi (20h^2-h^3)\\\\ & = (20)/(3) \pi h^2-\frac13 \pi h^3 \end{aligned}`

Part (c)

To find the value of h such that the volume of the cone is a maximum, differentiate V with respect to h:

`\begin{aligned}V & =(20)/(3) \pi h^2-\frac13 \pi h^3\\\\ \implies (dV)/(dh) & =2 \cdot (20)/(3) \pi h-3 \cdot \frac13 \pi h^2\\\\ & = (40)/(3) \pi h- \pi h^2\\\\ & = \pi h\left((40)/(3)-h\right)\end{aligned}`

Set it to zero:

`\begin{aligned}(dV)/(dh) & =0\\\\ \implies \pi h\left((40)/(3)-h\right) & = 0\end{aligned}`

Solve for h:

`\begin{aligned} \pi h & = 0 \implies h=0\\ (40)/(3)-h & =0\implies h=(40)/(3)\end{aligned}`

Substitute the found values of h into the equation for Volume:

`\begin{aligned}\textsf{when}\:h=0:V &=(20)/(3) \pi (0)^2-\frac13 \pi (0)^3\\\\ \implies V & =0\sf \:cm^3\end{aligned}`

`\begin{aligned}\textsf{when}\:h=(40)/(3):V &=(20)/(3) \pi \left((40)/(3)\right)^2-\frac13 \pi \left((40)/(3)\right)^3\\\\ \implies V & =(32000)/(27) \pi -(64000)/(81) \pi\\\\ & = (32000)/(81) \pi \\\\ & = 1241.123024..\sf \:cm^3\end{aligned}`

Therefore, the value of h such that the volume of the cone is a maximum is:

`h=(40)/(3)`

Answer 2

Cone details:

• height: h cm

• radius: r cm

Sphere details:

• radius: 10 cm

================

From the endpoints (EO, UO) of the circle to the center of the circle (O), the radius is will be always the same.

Using Pythagoras Theorem

(a)

TO² + TU² = OU²

(h-10)² + r² = 10² [insert values]

r² = 10² - (h-10)² [change sides]

r² = 100 - (h² -20h + 100) [expand]

r² = 100 - h² + 20h -100 [simplify]

r² = 20h - h² [shown]

r = √20h - h² ["r" in terms of "h"]

(b)

volume of cone = 1/3 * π * r² * h

===========================

`\longrightarrow \sf V = (1)/(3) * \pi * (√(20h - h^2))^2 \ ( h)`

`\longrightarrow \sf V = (1)/(3) * \pi * (20h - h^2) (h)`

`\longrightarrow \sf V = (1)/(3) * \pi * (20 - h) (h) ( h)`

`\longrightarrow \sf V = (1)/(3) \pi h^2(20-h)`

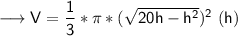
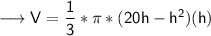
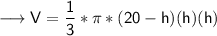
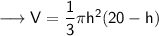
To find maximum/minimum, we have to find first derivative.

(c)

First derivative

`\Longrightarrow \sf V' =(d)/(dx) ( (1)/(3) \pi h^2(20-h) )`

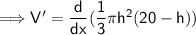
apply chain rule

`\sf \Longrightarrow V'=(\pi \left(40h-3h^2\right))/(3)`

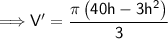
Equate the first derivative to zero, that is V'(x) = 0

`\Longrightarrow \sf (\pi \left(40h-3h^2\right))/(3)=0`

`\Longrightarrow \sf 40h-3h^2=0`

`\Longrightarrow \sf h(40-3h)=0`

`\Longrightarrow \sf h=0, \ 40-3h=0`

`\Longrightarrow \sf h=0,\:h=(40)/(3)`

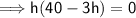
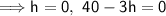
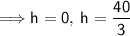
maximum volume: when h = 40/3

`\sf \Longrightarrow max= (1)/(3) \pi ((40)/(3) )^2(20-(40)/(3) )`

`\sf \Longrightarrow maximum= 1241.123 \ cm^3`

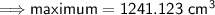
minimum volume: when h = 0

`\sf \Longrightarrow min= (1)/(3) \pi (0)^2(20-0)`

`\sf \Longrightarrow minimum=0 \ cm^3`