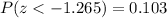Question

The mean annual income for people in a certain city (in thousands of dollars) is 42, with a standard deviation of 30. A pollster draws a sample of 90 people to interview. a. What is the probability that the sample mean income is less than 38?

Answer 1

`P(\bar X <38)`

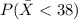
And we can use the z score formula given by:

`z = (\bar X -\mu)/((\sigma)/(√(n)))`

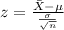
And if we find the z score for 38 we got:

`z = (38-42)/((30)/(√(90)))= -1.265`

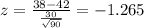
So then we want to find this probability:

`P(z<-1.265)`

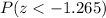
And we can use the normal standard distribution or excel and we got:

`P(z<-1.265)=0.103`

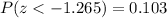
Explanation:

For this case we define the random variable X as the annual income for people at certain city. And we know the following properties:

`E(X) = 42, Sd(X) =42`

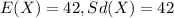
They select a sample size of n = 90>30. So then we can assume that the central limit can be applied.

From the central limit theorem we know that the distribution for the sample mean
`\bar X` is given by:

`\bar X \sim N(\mu, (\sigma)/(√(n)))`

We want to calculate this probability:

`P(\bar X <38)`

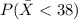
And we can use the z score formula given by:

`z = (\bar X -\mu)/((\sigma)/(√(n)))`

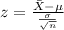
And if we find the z score for 38 we got:

`z = (38-42)/((30)/(√(90)))= -1.265`

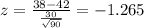
So then we want to find this probability:

`P(z<-1.265)`

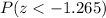
And we can use the normal standard distribution or excel and we got:

`P(z<-1.265)=0.103`