Question

An actor invested some money at 5% simple interest, and $41,000 more than 4 times the amount at 9%. The total annual interest earned from the investment was $35,260. How much did he invest at 5% and 9%?

Answer 1

• The amount invested at 5%=$77,000
• The amount invested at 9%=$349,000

Explanation:

• Let the amount invested at 5% simple interest =$x

He invested $41,000 more than 4 times the amount at 9%.

• This amount is: $(4x+41000)

Total Annual Interest Earned = $35,260

Therefore, Time=1 year

Simple Interest
`=(Principal X Rate X Time)/(100)`

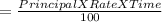
Therefore, his total interest

=Interest from Investment 1 + Interest from Investment 2

`35260=\left((x*5*1)/(100) \right)+\left((4x+41000*9*1)/(100) \right)\\35260=0.05x+(0.36x+3690)\\35260-3690=0.05x+0.36x\\31570=0.41x\\\text{Divide both sides by 0.41}\\x=\$77000`

Therefore:

The amount invested at 5%=$77,000

The amount invested at 9%=$(4*77,000+41000)=$349,000