Question

The probability density function of the time to failure of an electronic component in a copier (in hours) is f(x)= e^-x/100 /1000. Determine the probability that

a. A component lasts more than 3000 hours before failure.


b. A component fails in the interval from 1000 to 2000 hours.


c. A component fails before 1000 hours


d. Determine the number of hours at which 10% of all components have failed.


e. Determine the cumulative distribution function for the distribution. Use the cumulative distribution function to determine the probability that a component lasts more than 3000 hours before failure.

Answer 1

Check the explanation

Explanation:

The fundamentals

A continuous random variable can take infinite values in the range associated function of that variable. Consider
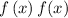`f\left( x \right)f(x)` is a function of a continuous random variable within the range
`\left[ {a,b} \right][a,b]` , then the total probability in the range of the function is defined as:

`\int\limits_a^b {f\left( x \right)dx} = 1 a∫b​ f(x)dx=1`

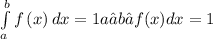
The probability of the function
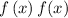`f\left( x \right)f(x)` is always greater than 0. The cumulative distribution function is defined as:

`F\left( x \right) = P\left( {X \le x} \right)F(x)=P(X≤x)`

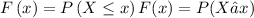
The cumulative distribution function for the random variable X has the property,

`0 \le F\left( x \right) \le 10≤F(x)≤1`

The probability density function for the random variable X has the properties,

`\\\begin{array}{c}\\{\rm{ }}f\left( x \right) \ge 0\\\\\int\limits_( - \infty )^\infty {f\left( x \right)dx} = 1\\\\P\left( E \right) = \int\limits_E {f\left( x \right)dx} \\\end{array} f(x)≥0`

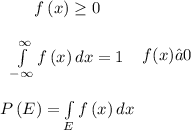
Kindly check the attached image below to see the full explanation to the question above.