Question

The range of F(x) = logbx is the set of all positive real numbers.

O A. True

O B. False

Answer 1

This is is TRUE :)

Answer 2

The range of F(x) = logbx is the set of all positive real numbers is TRUE

Explanation:

Given:

A function which logarithmic i.e F(x)=logbX=logx/logb with base 10

To Find;

Range belongs to All set are positive real numbers.

Solution:

The domain is function for which all set of inputs are defined and range for function is that set of all output that functions takes.

So Simple logarithmic function y=logbX is

`X=b^y`

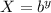
So The functions has domain of all real values and range set of all real number.

In general the function F(x) = logbx where X>0 and b≠1 is continuous and one to one function.

logarithmic function is not defined for negative numbers or for zero.

And Also function approaches y-axis as x-tends to infinity but never touches the it.

Hence the Given statement is true