Question

The length of a rectangular prism is 1 more than three times the width w. The volume of the prism is 3 w cubed plus 19 w squared plus 6 w. What is a simplified expression for the height of the​ prism?

Answer 1

Let w represent width of the rectangle.

We have been given that the length of a rectangular prism is 1 more than three times the width w. So length of the rectangle would be
`3w+1`.

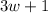We have been given that the volume of the prism is
`3w^3+19w^2+6w`.

We know that volume of rectangular prism is width times length times height.

So we can set an equation as:

`\text{Length}* \text{Width}*\text{Height}=3w^3+19w^2+6w`

`w(3w+1)*\text{Height}=3w^3+19w^2+6w`

`\text{Height}=(3w^3+19w^2+6w)/(w(3w+1))`

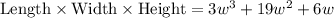
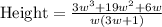
Let us factor out w from numerator.

`\text{Height}=(w(3w^2+19w+6))/(w(3w+1))`

`\text{Height}=(3w^2+19w+6)/(3w+1)`

`\text{Height}=(3w^2+18w+w+6)/(3w+1)`

`\text{Height}=(3w(w+6)+1(w+6))/(3w+1)`

`\text{Height}=((w+6)(3w+1))/(3w+1)`

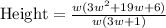
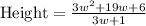
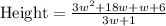
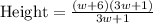
Now we will cancel out
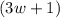`(3w+1)` from numerator and denominator.

`\text{Height}=w+6`

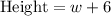
Therefore, the height of the prism is
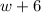`w+6` units.