Question

Maggies living room is the shape of a rectangle its dimensions are 21’ x 40’ what is the length of the diagonal rounded answer to the nearest 10th if necessary

Answer 1

The length of the diagonal is
`45.2^(')`

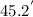
Explanation:

In this question, we are concerned with calculating the length of the diagonal of the room.

Mathematically, we need top picture a right-angled triangle where the diagonal is the hypotenuse and the length and width of the rectangle represents the other sides of the triangle

Since it is a right-angled triangle, we shall use Pythagoras' theorem to calculate the length of the diagonal. Let us call this d

Mathematically;

`d^(2) = 21^(2) + 40^(2)`

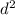`d^(2)` = 441 + 1600

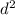`d^(2)` = 2041

d =
`√(2041)`

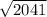
d = 45.18 inch which is 45.2 inch to the nearest tenth