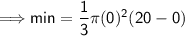Cone details:
Sphere details:
================
From the endpoints (EO, UO) of the circle to the center of the circle (O), the radius is will be always the same.
Using Pythagoras Theorem
(a)
TO² + TU² = OU²
(h-10)² + r² = 10² [insert values]
r² = 10² - (h-10)² [change sides]
r² = 100 - (h² -20h + 100) [expand]
r² = 100 - h² + 20h -100 [simplify]
r² = 20h - h² [shown]
r = √20h - h² ["r" in terms of "h"]
(b)
volume of cone = 1/3 * π * r² * h
===========================
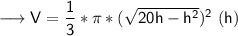
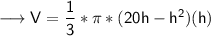
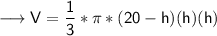
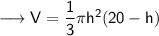
To find maximum/minimum, we have to find first derivative.
(c)
First derivative
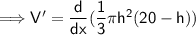
apply chain rule
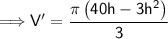
Equate the first derivative to zero, that is V'(x) = 0
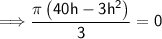
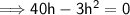
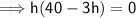
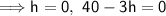
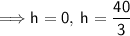
maximum volume: when h = 40/3
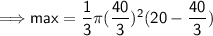
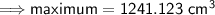
minimum volume: when h = 0