Answer:
q = 4870.0524 W
Step-by-step explanation:
Given that:
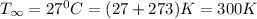
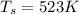

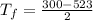
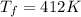
From Table A4; Thermophysical Properties of Gases at Atmospheric Temperature; Properties of air at film Temperature are as follows:
density
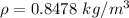
kinematic viscosity (v) =
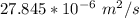
thermal conductivity K =
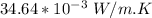
Prandtl number (Pr) = 0.689
Given that :
the length of the plate is = 150 cm = 1.5 m
the width of the plate = 10 cm = 0.1 m
Then the Area = W×L = 1.5 × 0.10 = 0.15 m²
Air flow velocity
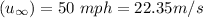
The Reynolds number
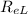 is calculated by using the formula :
is calculated by using the formula :
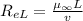

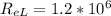 turbulent flow.
turbulent flow.
Thus, we can say that the turbulent flow is throughout the entire plate. Therefore, the appropriate correlation is addressed via the Nusselt number;
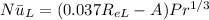
where;

and
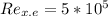
Then;
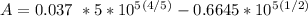
A = 871
Now;
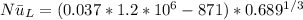
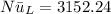
We can now determine the convention coefficient since the
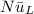 is known. By using the equation;
is known. By using the equation;
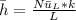
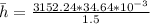
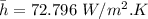
Finally the rate of heat removal q from both cooling surface of the plate (fin) is calculated as:
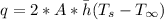
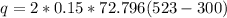
q = 4870.0524 W