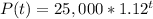Question

The town of Madison has a population of 25000 The population is increasing by a factor of 1.12 each year.

Write a function that gives the population P(t) in Madison t years from now.

Answer 1

`P(t)=25000(1.12)^(t)`

Explanation:

• The town has a population of 25000.
• The population is increasing by a factor of 1.12 each year.

This is a geometric progression since it increases by a factor.

The nth term of a geometric sequence is given by the function:

`U_n=ar^(n-1), $ where a=first term, r=common factor`

Since, we the growth starts from the second year, the function that gives the population P(t) in Madison t years from now therefore is:

`P(t)=25000(1.12)^(t)`

Answer 2

`P(t) = 25,000*1.12^t`

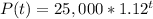
Explanation:

The populational growth is exponential with a factor of 1.12 each year. An exponential function has the following general equation:

`y(x) = ab^x`

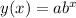
Where 'a' is the initial population (25,000 people), 'b' is the growth factor (1.12 per year), 'x' is the time elapsed, in years, and 'y(x)' is the population after 'x' years.

Therefore, the function P(t) that models the population in Madison t years from now is:

`P(t) = 25,000*1.12^t`