Question

Between the years of 1947 and 1956 earthenware jars containing what are known as the Dead Sea scrolls were found in caves along the coast of Jerusalem in the Dead Sea. Upon radiometric testing it was found that the scrolls were wrapped in material that contained about 79 percent of the original carbon-14.archeologists estimated that the scrolls are about 1900 years old. Are they right ?

Answer 1

The hypothesis is correct.

Explanation:

Using the half-life equation, the number of years (1,900) can be substituted for t and the half-life (5,730) can be substituted for h. Since the original amount is not known but the percent remaining is known, any value can be used for the original amount. Using 100 will be the easiest. Plugging these values into the equation gives 79.47 remaining. If 79.47 of the original 100 units are left, that is 79.47 percent. Since radiometric dating gives an estimate of age, the archeologists’ hypothesis is correct.

Answer 2

The scroll is 1949 years old, thus the archeologists are right.

Explanation:

The decay equation of ¹⁴C is:

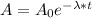`A = A_(0)e^(-\lambda*t)` (1)

Where:

A₀: is the initial activity

A: is the activity after a time t = 79%*A₀

λ: is the decay rate

The decay rate is:

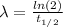`\lambda = (ln(2))/(t_(1/2))` (2)

Where
`t_(1/2)`: is the half-life of ¹⁴C = 5730 y

By entering equation (2) into equation (1) we can find the age of the scrolls.

`A = A_(0)e^(-\lambda*t) = A_(0)e^{-(ln(2))/(t_(1/2))*t}`

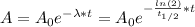
Since, A = 79%*A₀, we have:

`(79)/(100)A_(0) = A_(0)e^{-(ln(2))/(t_(1/2))*t}`

`ln((79)/(100)) = -(ln(2))/(t_(1/2))*t`

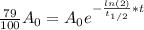
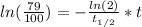
Solving the above equation for t:

`t = -(ln(79/100))/((ln(2))/(t_(1/2)))`

`t = -(ln(75/100))/((ln(2))/(5730 y)) = 1949 y`

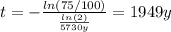
Hence, the scroll is 1949 years old, thus the archeologists are right.

I hope it helps you!