Question

Historically, voter turnout for political elections in Texas have been reported to be 54%. You have been assigned by a polling company to test the hypothesis that voter turnout during the most recent election was higher than 54%. You have collected a random sample of 90 registered voters from this elections and found that 54 actually voted. Assume that the true proportion of voter turnout is 0.67. Calculate the probability of a Type II error using α= 0.02.

Answer 1

The probability of a Type II error is 0.3446.

Explanation:

A type II error is a statistical word used within the circumstance of hypothesis testing that defines the error that take place when one is unsuccessful to discard a null hypothesis that is truly false. It is symbolized by β i.e.

β = Probability of accepting H₀ when H₀ is false

= P (Accept H₀ | H₀ is false)

In this case we need to test the hypothesis whether the voter turnout during the most recent elections in Texas was higher than 54%.

The hypothesis can be defined as:

H₀: The voter turnout during the most recent elections in Texas was 54%, i.e. p = 0.54.

Hₐ: The voter turnout during the most recent elections in Texas was higher than 54%, i.e. p > 0.54.

A type II error would be committed if we conclude that the voter turnout during the most recent elections in Texas was 54%, when in fact it was higher.

The information provided is:

X = 54

n = 90

α = 0.02

true proportion = p = 0.67

Compute the mean and standard deviation as follows:

`\mu=p=0.54`

`\sigma=\sqrt{(0.54(1-0.54))/(90)}=0.053`

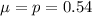
Acceptance region = P (Z < z₀.₀₂)

The value z₀.₀₂ is 0.6478.

Compute the sample proportion as follows:

`z=(\hat p-\mu)/(\sigma)\\2.054=(\hat p-0.54)/(0.053)\\\hat p=0.6489`

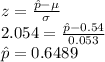
Compute the value of β as follows:

β = P (p < 0.54 | p = 0.67)

`=P((\hat p-\mu)/(\sigma)<(0.6489-0.67)/(0.053))\\=P(Z<-0.40)\\=0.34458\\\approx 0.3446`

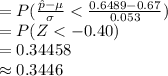
Thus, the probability of a Type II error is 0.3446.