Question

From a circular cylinder of diameter 10 cm and height 12 cm are conical cavity of the same base radius and of the same height is hollowed out. Find the volume and the whole surface of the remaining solid.


`(take \ \: \pi \: = 3.14)`


​

Answer 1

Volume of the remaining solid = 628 cm^2

Whole surface area = 659.4 cm^2

Explanation:

Now, Given that:-

Diameter (d) = 10 cm

So, Radius (r) = 10/2 = 5cm

Height of the cylinder = 12cm.

`volume \: of \: the \: cylinder \: = \pi {r}^(2) h`

`= > \pi * {5}^(2) * 12 {cm}^(3) = 300\pi {cm}^(3)`

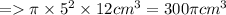
Radius of the cone = 5 cm.

Height of the cone = 12 cm.

`slant \: height \: of \: the \: cone \: = \sqrt{ {h}^(2) + \: {r}^(2) }`

`= > \sqrt{ {5}^(2)+{12}^(2) } cm \: = 13cm`

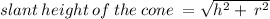
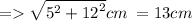
Volume of the cone = 1/3 *πr^2h

`= > (1)/(3) \pi * {5}^(2) * 12 {cm}^(3) = 100\pi {cm}^(3)`

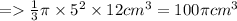
therefore, the volume of the remaining solid

`= 300\pi {cm}^(3) - 100\pi {cm}^(3) \\ = 200 * 3.14 {cm}^(3) = 628 {cm}^(3)`

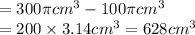
Curved surface of the cylinder =

`2\pi \: rh \: = 2\pi * 5 * 12 {cm}^(2) \\ = 120\pi {cm}^(2) .`

`curved \: surface \: of \: the \: cone \: = \pi \: rl \\ = \pi * 5 * 13 {cm}^(2) \\ = 65\pi {cm }^(2) \\ area \: of \: (upper)circular \: base \: \\ of \: cylinder \: = \\ = \pi \: {r}^(2) = \pi * {5}^(2)`

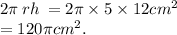
therefore, The whole surface area of the remaining solid

= curved surface area of cylinder + curved surface area of cone + area of (upper) circular base of cylinder

`= 120\pi {cm}^(2) + 65\pi {cm }^(2) + 25 \pi {cm}^(2) \\ = 210 * 3.14 {cm}^(2) = 659.4 {cm}^(2)`

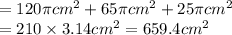
Hope it helps you!!