Answer:
Explanation:
Let represent the edge of the tank with x and the radius of the first sphere with x/2;
The amount of the water = Volume of the tank - Volume of the sphere
=
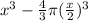
on the second cube ; the radius of the sphere =
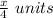 ;
;
Also the number of sphere here is = 8
The amount of water =
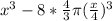
For the third figure ; the radius of the sphere is =
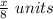
Also the number of sphere here is = 64
The amount of water =
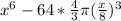
=
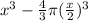
In the fourth tank ; 512 sphere illustrates that in a single row; that more than one 8 sphere is present i.e 8³ = 512
then the radius will be =

The amount of water =

=
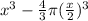
This implies that alll the three cube shaped tanks are identical and hold equal amount of water.