Answer:
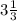 or
or
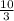
Explanation:
We could use the combined rate equation to find the combined rate of work.
Combined rate of work formula:
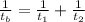 , where
, where
 is the individual time for object A,
is the individual time for object A,
 the individual time for object B and
the individual time for object B and
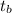 is the time for A and B together.
is the time for A and B together.
The time it takes Irina to paint the room alone,
 = 5 hours
= 5 hours
The time it takes Paulo to paint the room,
 = 10 hours
= 10 hours
1) Substitute object A (Irina) and B (Paulo) into the formula given above, and change
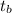 into an
into an
 .
.
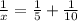
2) Add the fractions.
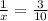
3) Solve for the
 .
.
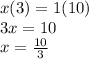
4) Change them into a mixed fraction.
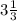
Note:
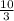 or
or
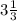 are both correct. Write the answer according to the question. In this case, there is no specific rule, so I choose
are both correct. Write the answer according to the question. In this case, there is no specific rule, so I choose
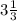 .
.