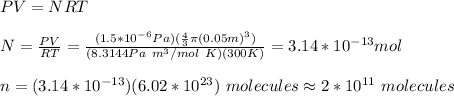Question

Very thin films are usually deposited under vacuum conditions to prevent contamination and ensure that atoms can fly directly from the source to the depositing surface without being scattered along the way.

a. To get an idea of how few and far between the air molecules are in a thin-film deposition chamber, determine the mean free path of a generic "air" molecule with an effective diameter of 0.25 nm at a pressure of 1.5 x 10-6 Pa and temperature of 300 K.


b. If the chamber is spherical with a diameter of 10 cm, estimate how many times a given molecule will collide with the chamber before colliding with another air molecule.


c. How many air molecules are in the chamber (treating "air" as an ideal gas)?

Answer 1

a. 9947 m

b. 99476 times

c. 2*10^11 molecules

Step-by-step explanation:

a) To find the mean free path of the air molecules you use the following formula:

`\lambda=(RT)/(√(2)\pi d^2N_AP)`

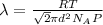
R: ideal gas constant = 8.3144 Pam^3/mol K

P: pressure = 1.5*10^{-6} Pa

T: temperature = 300K

N_A: Avogadros' constant = 2.022*10^{23}molecules/mol

d: diameter of the particle = 0.25nm=0.25*10^-9m

By replacing all these values you obtain:

`\lambda=((8.3144 Pa m^3/mol K)(300K))/(√(2)\pi (0.25*10^(-9)m)^2(6.02*10^(23))(1.5*10^(-6)Pa))=9947.62m`

b) If we assume that the molecule, at the average, is at the center of the chamber, the times the molecule will collide is:

`n_(collision)=(9947.62m)/(0.05m)\approx198952\ times`

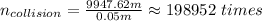
c) By using the equation of the ideal gases you obtain:

`PV=NRT\\\\N=(PV)/(RT)=((1.5*10^(-6)Pa)((4)/(3)\pi(0.05m)^3))/((8.3144Pa\ m^3/mol\ K)(300K))=3.14*10^(-13)mol\\\\n=(3.14*10^(-13))(6.02*10^(23))\ molecules\approx2*10^(11)\ molecules`