Question

A storekeeper wants to mix two types of flour to get 300 pounds, so he can sell it by 2.50$ per pound. If he uses flour worth $2.40 a pound with another flour worth $3.00 a pound, how many pounds of each does he use?

Answer 1

50lb of 3.00

250lb of 2.40

Explanation:

Answer 2

90 pounds, 210 pounds

Explanation:

Given:

A storekeeper wants to mix two types of flour to get 300 pounds, so he can sell it by 2.50$ per pound.

He uses flour worth $2.40 a pound with another flour worth $3.00 a pound.

Question:

How many pounds of each does he use?

Solution:

Let pounds of one type of flour mixed =
`x`

Then pounds of another type of flour mixed =
`300-x`

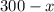
Cost of 1 pound of one type of flour = $2.40

Cost of
`x` pounds of one type of flour =
`2.4x`

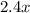
Similarly,

Cost of 1 pound of another type of flour = $3

Cost of
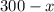`300-x` pounds of another type of flour =
`3(300-x)=900-3x`

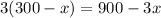
Cost of mixed flour per pound = $2.5

Total cost of mixed flour per pound = $2.5
`*` 300 = $750

Cost of
`x` pounds of one type + Cost of
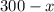`300-x` pounds of another type = $750

`2.4x+900-3x=750\\\\ -0.6x+900=750\\ \\ Subtracting\ both\ sides\ by\ 900\\ \\ -0.6x+900-900=750-900\\ \\ -0.6x=-150\\ \\ Minus\ canceled\ by\by\ minus\\ \\ 0.6x=150\\ \\ Dividing\ both\ sides\ by\ 0.6\\ \\ x=90`

Pounds of one type of flour mixed =
`x` = 90 pounds

Pounds of another type of flour mixed =
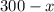`300-x` = 300 - 90 = 210 pounds

Thus, 90 pounds of one and 210 pound of another type of flour mixed.