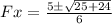Question

Carlos is using the quadratic formula to find the solutions of y=3x^2-5x-2. Which of the following will simplify to the correct solutions? (options on photo)

Answer 1

`Fx=(5\pm√(25+24) )/(6)`

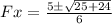
Explanation:

A quadratic equation in one variable given by the general expression:

`ax^2+bx+c`

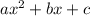
Where:

`a\\eq 0`

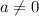
The roots of this equation can be found using the quadratic formula, which is given by:

`x=(-b\pm√(b^2-4ac) )/(2a)`

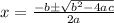
So:

`y(x)=3x^2-5x-2=0`

As you can see, in this case:

`a=3\\b=-5\\c=-2`

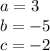
Using the quadratic formula:

`x=(-b\pm√(b^2-4ac) )/(2a)=(-(-5)\pm√((-5)^2-4(3)(-2)) )/(2(3))=(5\pm√(25+24) )/(6)`

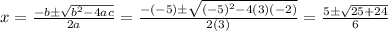
Therefore, the answer is:

`Fx=(5\pm√(25+24) )/(6)`