Answer:
95% confidence interval for the difference in the proportion is [-0.017 , 0.697].
Explanation:
We are given that a simple random sample of 12 small cars were subjected to a head-on collision at 40 miles per hour. Of them 8 were "totaled," meaning that the cost of repairs is greater than the value of the car.
Another sample of 15 large cars were subjected to the same test, and 5 of them were totaled.
Firstly, the pivotal quantity for 95% confidence interval for the difference between population proportion is given by;
P.Q. =
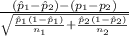 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of small cars that were totaled =
= sample proportion of small cars that were totaled =
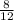 = 0.67
= 0.67
 = sample proportion of large cars that were totaled =
= sample proportion of large cars that were totaled =
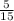 = 0.33
= 0.33
 = sample of small cars = 12
= sample of small cars = 12
 = sample of large cars = 15
= sample of large cars = 15
 = population proportion of small cars that are totaled
= population proportion of small cars that are totaled
 = population proportion of large cars that were totaled
= population proportion of large cars that were totaled
Here for constructing 95% confidence interval we have used Two-sample z proportion statistics.
So, 95% confidence interval for the difference between population population, (
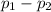 ) is ;
) is ;
P(-1.96 < N(0,1) < 1.96) = 0.95 {As the critical value of z at 2.5% level
of significance are -1.96 & 1.96}
P(-1.96 <
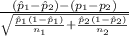 < 1.96) = 0.95
< 1.96) = 0.95
P(
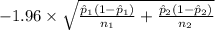 <
<
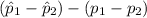 <
<
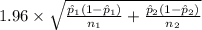 ) = 0.95
) = 0.95
P(
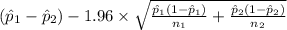 <
<
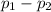 <
<
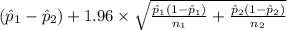 ) = 0.95
) = 0.95
95% confidence interval for
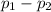 = [
= [
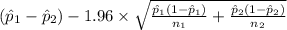 ,
,
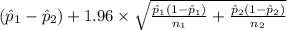 ]
]
= [
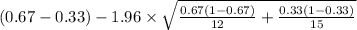 ,
,
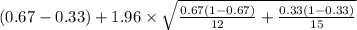 ]
]
= [-0.017 , 0.697]
Therefore, 95% confidence interval for the difference between proportions l and 2 is [-0.017 , 0.697].