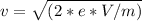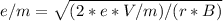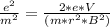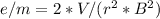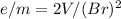Question

Derivation of Eq. (3): o Basic physics principles: Justify equations (1) and (2) in your own words. . Doing the algebra: From equations (1) and (2), show that equation (3) holds. mu? =eu B This would be nice if we knew the velocity. Fortunately, we know the voltage through which the electrons are accelerated. Setting the change in electrical potential energy equal to the final kinetic energy of the electrons, we find: eV = From this point, some algebra lets us eliminate the velocity variable entirely, giving us: e 2V m (B_T)

Answer 1

About eq (1)

`mv^2/r = eVB`

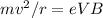
when a charged particle (electron) enters into the magnetic field which is perpendicular to direction of motion than there will be magnetic force on particle and particle will travel in circular path in with constant speed.

So using force balance on charged particle:

`F_(net) = Fc - Fm`

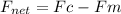
Since particle is traveling at constant speed, So acceleration is zero, and

`F_(net) = 0`

`Fc - Fm=0`

`Fc = Fm`

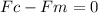
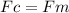
Fc = centripetal force on particle
`= m*v^2/r`

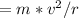
Fm = magnetic force on electron =
`q*VxB = q*V*B*sin \theta`

q = charge on electron = e

since magnetic field is perpendicular to the velocity of particle, So theta = 90 deg

sin 90 deg = 1

So,

`m*v^2/r = e*v*B`

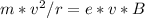
About equation 2:

When this charged particle is released from rest in a potential difference V, and then it enters into above magnetic field, then using energy conservation on charge particle

`KEi + PEi = KEf + PEf`

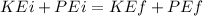
KEi = 0, since charged particle started from rest

`PEi - PEf = q*dV`

`PEi - PEf = eV`

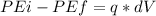
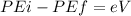
KEf = final kinetic energy of particle when it leaves
`= (1/2)*m*v^2`

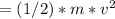
So,

`0 + eV = (1/2)*m*v^2`

`eV = (1/2)*m*v^2`

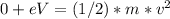
From above equation (1) and (2)

`m*v^2/r = evB`

`e/m = v/(r*B)`

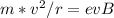
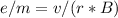
Now

`eV = (1/2)*m*v^2`

`v = √((2*e*V/m))`

`e/m = √( (2*e*V/m)/(r*B))`

`(e^2)/(m^2) = (2*e*V)/((m*r^2*B^2))`

`e/m = 2*V/(r^2*B^2)`

`e/m = 2V/(Br)^2`