Question

The half-life of caffeine is 5 hours. If you ingested a 30 oz Big Gulp, after how much time will have to pass before you have under 1 oz of caffeine remaining?

Answer 1

The time that will have to pass before one has under 1 oz of caffeine remaining is 24.53 hours

Step-by-step explanation:

Here, we have the formula for half life as follows;

`N(t) = N_0((1)/(2))^{(t)/(t_(1/2))`

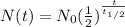
Where:

N(t) = Remaining quantity of the substance = 1 oz

N₀ = Initial quantity of the substance = 30 oz

t = Time duration

`t_(1/2)` = Half life of the substance = 5 hours

Therefore, plugging in the values, we have

`1= 30((1)/(2))^{(t)/(5)}`

`(1)/(30) = ((1)/(2))^{(t)/(5)}\\ln((1)/(30)) =(t)/(5) ln((1)/(2))\\(t)/(5) = (ln((1)/(30)) )/( ln((1)/(2))) = 4.91\\ t = 4.91 * 5 = 24.53 \ hours`

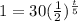
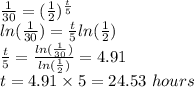
The time that will have to pass before one has under 1 oz of caffeine remaining = 24.53 hours.