Answer:
Explanation:
Hello!
Text from Exercise 1:
"The waking times (in minutes past 5:00 a.m.) of 40 people who start work at 8:00 a.m. are shown in the table at the left. Assume the population standard deviation is 45 minutes."
The study variable is X: waking time (past 5:00 a.m.) of one person, measured in minutes.
Assuming the variable has a normal distribution, the margin of error, d, of the CI for the population mean waking time is:
d=
 * (δ/√n)
* (δ/√n)
You have to calculate the sample size for a 95% CI, σ= 45min and d=10 min.
For this you have to clear the sample size from the formula:
d=
 * (δ/√n)
* (δ/√n)
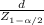 =δ/√n
=δ/√n
√n*
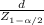 = δ
= δ
√n= δ *
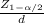
n= ( δ *
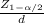 )²
)²
n= (45*
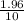 )²
)²
n= 77.79≅ 78
You need a sample of at least 78 people to estimate the population mean of the waking time using a 95% CI.
I hope this helps!