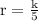Answer and explanation:
z = 5r represents cone
in the plane z = k (k > 0)
k=5r
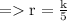
The equation says that the z-value of each point on the surface is the same as five times r,
the distance from the point to the z-axis. Because θ doesn't appear, it can vary. So any horizontal trace in the plane z = k (k > 0) is a circle of radius