Question

Jade used candle molds, as shown, to make candles that were perfect cylinders and spheres:

A cylindrical mold is shown, the radius of the top circular section of the cylinder is labeled 3 inches and the height of the cylinder is labeled as 7 inches. On the right side of this mold is a spherical mold. The radius of this spherical mold is labeled as 3 inches.
What is the approximate difference in the amount of wax needed to make a candle from each of these molds? (Use π = 3.14.) (1 point)

Group of answer choices

27.0 cubic inches

47.1 cubic inches

84.78 cubic inches

91.12 cubic inches

Answer 1

The difference in the amount of wax needed is 84.78 in³ (84.78 cubic inches)

Explanation:

Given

Cylinder

Radius = 3 inches

Height = 7 inches

Sphere

Radius = 3 inches

Required

The difference in the amount of wax needed to make a candle from each of these molds

The quantity or amount required to make a wax of candle from each molds can be calculated by getting the volume of both molds

The volume of a cylinder is calculated using

V₁ = πr²h

where r and h are the radius and the height of the cylinder, respectively.

r = 3 in and h = 7 in

The volume of a sphere is calculated using

`V_(2) = (4)/(3)\pi r^3`

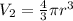
where r is the radius of the sphere

r = 3 in

Calculating V₁

V₁ = πr²h

V₁ = π * 3² * 7

V₁ = π * 9 * 7

V₁ = π * 63

V₁ = 63π

Calculating V₂

`V_(2) = (4)/(3)\pi r^3`

`V_(2) = (4)/(3) * \pi * 3^3`

`V_(2) = (4)/(3) * \pi * 27`

`V_(2) = (108)/(3) * \pi`

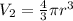
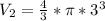
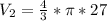
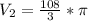
V₂ = 36π

Having calculated the volume of each molds, the difference in the amount of wax needed can then be calculated.

Difference = V₁ - V₂

Substituting 63π for V₁ and 36π for V₂

Difference = 63π - 36π

Difference = 27π

(Taking π = 3.14)

Difference = 27 * 3.14

Difference = 84.78

Hence, difference in the amount of wax needed is 84.78 in³