Question

For a quality control test, a company checks the miles per gallon (mpg) for a simple random sample of 100 minivans drawn from its current inventory. The average mpg of these 100 minivans is 15.6 with a standard deviation of 1.9 mpg. Set up an approximate 95% confidence interval for the average mpg of all minivans in the company's inventory.Select only one of the boxes below.A. It is appropriate to compute a confidence interval for this problem using the Normal curve.B. The Normal curve cannot be used to make the requested confidence interval.C. Making the requested confidence interval does not make any sense.If it is appropriate to compute a confidence interval for this problem using the Normal curve, then enter the confidence interval below. Otherwise, enter [0,0] for the confidence interval.

Answer 1

95% confidence interval for the average mpg of all minivans in the company's inventory is [15.22 mpg , 15.98 mpg].

Explanation:

We are given that a company checks the miles per gallon (mpg) for a simple random sample of 100 minivans drawn from its current inventory.

The average mpg of these 100 minivans is 15.6 with a standard deviation of 1.9 mpg.

Firstly, the pivotal quantity for 95% confidence interval for the population mean is given by;

P.Q. =
`(\bar X -\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

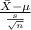where,
`\bar X` = sample average mpg = 15.6 mpg

s = sample standard deviation = 1.9 mpg

n = sample of minivans = 100

`\mu` = population average mpg

Here for constructing 95% confidence interval we have used One-sample t test statistics because we don't know about population standard deviation.

So, 95% confidence interval for the population mean,
`\mu` is ;

P(-1.987 <
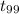`t_9_9` < 1.987) = 0.95 {As the critical value of t at 99 degree

of freedom are -1.987 & 1.987 with P = 2.5%}

P(-1.987 <
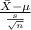`(\bar X -\mu)/((s)/(√(n) ) )` < 1.987) = 0.95

P(
`-1.987 * {(s)/(√(n) ) }` <
`{\bar X -\mu}` <
`1.987 * {(s)/(√(n) ) }` ) = 0.95

P(
`\bar X-1.987 * {(s)/(√(n) ) }` <
`\mu` <
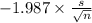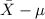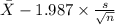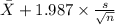`\bar X+1.987 * {(s)/(√(n) ) }` ) = 0.95

95% confidence interval for
`\mu` = [
`\bar X-1.987 * {(s)/(√(n) ) }` ,
`\bar X+1.987 * {(s)/(√(n) ) }` ]

= [
`15.6-1.987 * {(1.9)/(√(100) ) }` ,
`15.6+1.987 * {(1.9)/(√(100) ) }` ]

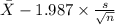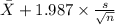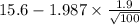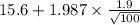= [15.22 mpg , 15.98 mpg]

Therefore, 95% confidence interval for the average mpg of all minivans in the company's inventory is [15.22 mpg , 15.98 mpg].

It is appropriate to compute a confidence interval for this problem using the Normal curve as t test statistics is used when data should follow normal distribution.