Answer:
The percentage of admitted applicants who had a Math SAT of 700 or more is 48.48%.
Explanation:
The Bayes' theorem is used to determine the conditional probability of an event E
 , belonging to the sample space S = (E₁, E₂, E₃,...Eₙ) given that another event A has already occurred by the formula:
, belonging to the sample space S = (E₁, E₂, E₃,...Eₙ) given that another event A has already occurred by the formula:
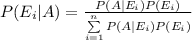
Denote the events as follows:
X = an student with a Math SAT of 700 or more applied for the college
Y = an applicant with a Math SAT of 700 or more was admitted
Z = an applicant with a Math SAT of less than 700 was admitted
The information provided is:
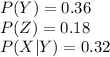
Compute the value of
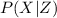 as follows:
as follows:
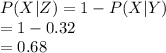
Compute the value of P (Y|X) as follows:
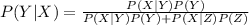
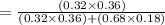
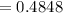
Thus, the percentage of admitted applicants who had a Math SAT of 700 or more is 48.48%.